Binomial cube
<videoflash>D9Bvi00xlns&NR</videoflash>
Contents
Age
3-6
Materials
A box containing eight wooden blocks:
- One red cube
- One blue cube
- Three red and black rectangular prisms
- Three blue and black rectangular prisms
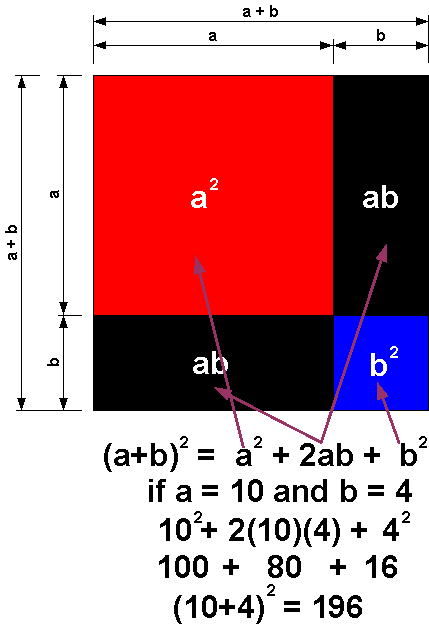
All the blocks fit into a natural wood box. Each side of the cube has the same dimensions and pattern, and represents the square of (a + b). The faces of the small blocks are color coded: a2 is always red, b2 is always blue, and "ab" is always black.
Preparation
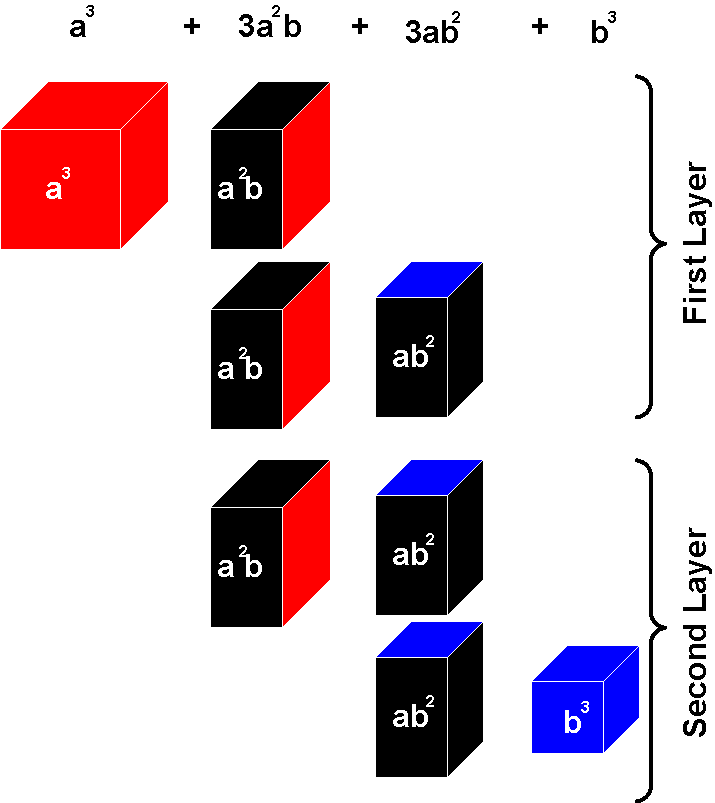
Algebraic expression: (a + b)3 = (a + b)(a + b)(a + b) = a3+3a2b+3ab2+b3
This is an individual exercise (Note: work cycle to be observed)
The child takes the cube apart beginning with b3 and lays out the pieces as shown, according to the formula.
The child reconstructs the cube, matching red faces, black faces, and blue faces, beginning with a3.
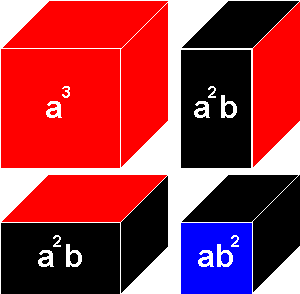
First Layer of the Binomial Cube: (represents a3+2a2b+ab2)
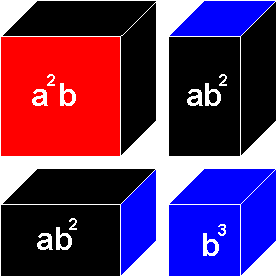
Second layer of the Binomial Cube: (represents a2b+2ab2+b3)
Presentation
- The Directress shows the child how to carry the box to the table. She sits besides the child, open up the box and lays out the blocks in the following pattern that will make it easy for rebuilding the cube in two layers.
- The Directress then shows the child how to rebuild the cube. The colors printed on the lid act as a guide.
Control Of Error
The color codes.
The cube can not be built if incorrectly assembled.
Points Of Interest
One way that humans attempt to survive is by understanding the world around them. The human brain is a pattern seeking organism. So, by nature, children are interested in finding patterns, relationships, and order. If children have worked their way through the materials for dimension, color, and shape, they will have found order, patterns, and relationships in those materials, and will have developed the ability to discriminate attributes to a point where they will enjoy the challenge of exploring the order inherent in the binomial and trinomial cubes. For this age, the purpose of the material is not to teach math, but instead, to provide a challenge for a child's ability to find patterns and relationships. Therefore, the material is presented as a sensorial activity. It is presented like a three dimensional puzzle. Anyone who likes to do puzzles knows that in order to master a puzzle, you have to pay attention to the relationship between the pieces. People who are masters at puzzles will tell you that they take out, and organize, puzzle pieces very carefully. This is what is modeled for the child in this activity.
The math presented above and below is provided for the teacher and is not to be presented or discussed with the child of this age. The math is presented to the children when they are older and are ready for it.
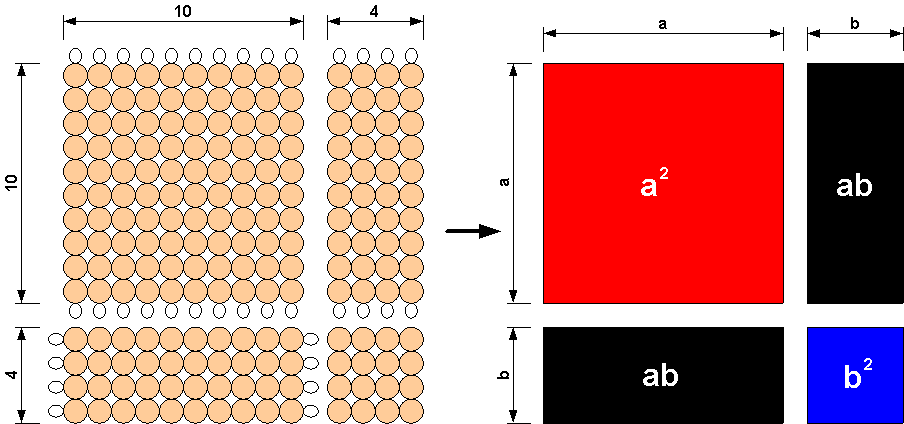
To firmly grasp the mathematical concepts behind the binomial cube, it's simplest if we start two dimensions instead of the three dimensions used by the binomial cube. .
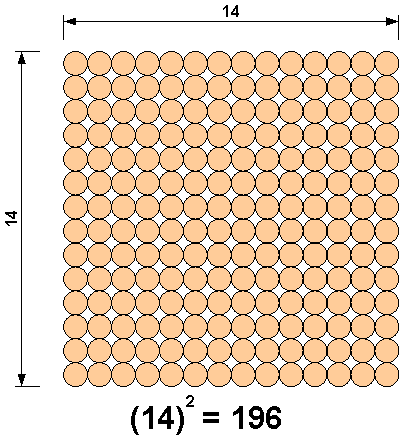
For this example, we start with golden beads. The image below shows how we would represent (10 + 4)2.
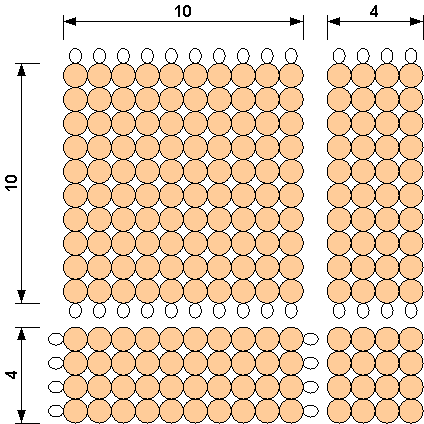
Now instead of beads, if we represent each block of beads as colored blocks as we do with the binomial cube, we get the figure below on the right. The number 10 here is represented by the variable "a", and the number 4 is represented by the variable "b".
The figure below explains the algebra behind the binomial cube.
Now if we go back to the beads, combining all blocks together, we get the following:
Purpose
- Provide the child with tangible experience of the way in which the cube can be divided and sub-divided.
- Lay the foundations for the later study of algebra.
- The child is at the stage of the absorbent mind. The child is not asked to understand the formula, but is using the cube in a mathematical way. The child will build up a predisposition to enjoy and understand mathematics later.
Variation
Handouts/Attachments